A4 - Watson, Tillman, LaChance

A supreme bridge can be defined as a bridge that can support a large amount of weight at a low cost.  That was the goal for this class.  Our job was to build the best bridge possible using K’Nex pieces.  A truss is a triangular joint that disperses weight.  Most bridges today are built with some sort of truss system.  Each week we were given a different assignment regarding bridges.  Throughout this course we would use software, online resources, pencil and paper, K’Nex and our minds to design a bridge.  Westpoint Bridge Designer is a popular bridge-design program that allows the user to create their own bridge and test it. The program displays results in the form of compression and tension forces acting on the designed bridge.  Bridge Designer was also used.  This program focuses heavily on forces of tension and compression acting on a bridge that the user sketches.  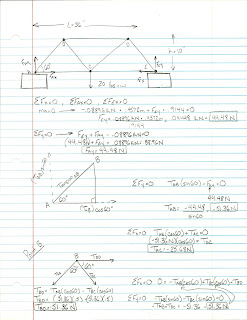One could also analyze forces acting on a bridge using the “Methods of Joints”.  This process requires the use of physics to calculate forces acting on joints.  The first bridge that needed to be built had to be at least two feet long.  This allowed us to get in some good bridge building experience before we started on our final design.  While building, it was suggested that cost be kept in mind because the cost to weight ratio is what the final bridge’s effectiveness will be determined by.  After the two-foot bridge was built, the next task was to construct a three-foot bridge.  This time, the bridge had to have a two-by-three inch hole running through the middle.  This constraint was implemented to simulate the construction of an actual bridge in which a passageway for transportation was necessary. As the term went on, each group member was responsible for posting entries on the team blog weekly.  These posts would answer a question determined by the professor each week and recap what had happened in or out of class during the previous week.

            From the beginning, the goal was to build a strong bridge and brainstorm ways to make it less expensive.  The team favored this approach because there was always a way to make the bridge support more weight and there were always ways to make the bridge less expensive.  This was not the most efficient approach because supporting the most weight does not always result in the best bridge.  The best way to build a bridge is to consider factors such as cost and strength, in the design planning.  To achieve success other small goals were set.  The team planned on meeting weekly to discuss our plans while moving further.  This was a good idea because it gave each member more time to brainstorm.  Another goal was to listen to and consider every idea.  When conflicting ideas arose, compromising is always the most effective solution.  Every goal that was established early in the course was met even though the final bridge outcome was somewhat of a disappointment.  The goal to build the strongest bridge possible and disregard cost was the only goal that was altered in the building process.  This method was abandoned because it would severely alter the cost-weight ratio and one design mistake could result in an unfavorable, high ratio. Our first bride design was ridiculously expensive.  More specifically it was the most expensive in the class.  This is the point where our goal changed.  For the second bridge design, which was the three-foot design, we had made cost efficiency a main priority along with strength.  The role of individual assignments was very helpful when compiling the final design.  These assignments made the group come up with as many bridge designs as possible so that best design could be chosen.  These assignments also help us get a better individual understanding of bridge design.  Westpoint Bridge Designer helped each member achieve a better understanding of what designs worked the most efficiently and which ones did not.  The force analysis and calculations brought to attention where significant force was being applied the most and where it was being applied the least.  The program also challenged each member to try and make an inexpensive bridge while also maintaining the bridge’s safety.  When the truss analysis was carried out, it again revealed areas on the bridge supporting large amounts of tension and compression.  In addition to using the program, each member also carried out calculations done by hand.  Each member’s individual designs produced the widest range of ideas.  This was helpful because the team was able to see which design was the most effective, then improving on the chosen design.  After testing the original bridge design, the structure bowed and the bridge failed.  When it was time to build the final bridge, the two most important objectives in mind were cost and failing weight.  The original bridge was incredibly expensive due to the large amount of pieces used.  To lower price, the team used longer members and fewer gusset plates. The three-foot-long final bridge ended up costing as much as the original two-foot bridge.  To avoid the bridge failing due to bowing to the side, additional trusses were placed in the center of the bridge.  At first when the final bridge was tested, it did not hold as much weight as was hoped.  As a result, an additional truss section was added to the top of the bridge for added stability.  This change resulted in the bridge’s ability to support another ten pounds.  The final design resembled a series of attached cubes with a top truss section.  The sides had trusses resembling X’s, held together by members that were perpendicular to the sides and trusses in the middle.  The predicted load at failure for the final bridge was about forty pounds.

Figure 1: Truss Analysis 

Figure 1.2: Truss Analysis Cont.

Figure 2: Bridge Designer

Figure 3: Westpoint Bridge Design

The three-foot bridge design was approached in a similar way as the two-foot bridge, except for minor changes to reduce cost. All grooved gusset plates were removed to significantly reduce overall cost. The design began as a simple truss bridge with X-shaped supports on the sides and an over truss section for added support. The bridge continued to be less stable than desired. Because of this, more pieces were added to the center. These added supports resulted in the doubling of the overall amount of weight the bridge was able to support.

Bill of Materials - Knex Pieces
Part Number				Description	Unit Cost ($)	Nr. of Parts	Cost ($)
1				1.25" long chord	$500	56	$28,000
2				2.125" long chord	$1,000	108	$108,000
3				3.375" long chord	$1,500	80	$120,000
4				5" long chord	$2,000	10	$20,000
5				7.5" long chord	$3,000	0	$0
6				chord splice	$1,000	0	$0
7				45 degree gusset plate	$1,000	0	$0
8				90 degree gusset plate	$1,000	0	$0
9				135 degree gusset plate	$1,000	0	$0
10				180 degree gusset plate	$1,000	108	$108,000
11				180 degree grooved gusset plate	$2,000	0	$0
12				360 degree gusset plate	$1,000	0	$0
13				360 degree grooved gusset plate	$2,000	0	$0
		Total Cost		$384,000

Figure 4: Bridge Sketch

Figure 5: Final Design

The bridge failed around 31 pounds. Instead of exploding into thousands of pieces, the bridge bowed out to the side. The bridge broke on the right side under the raised truss section, just as predicted. In a real life situation this would be preferred because bridge maintenance would be easier. Inspectors would know where to look if the bridge was failing.

Figure 6: Breaking Point

Figure 6.1: Breaking Point

After testing the final, three-foot bridge, it was determined that the bridge was able to support 42.3 pounds. The maximum amount of weight the bridge could support was tested by suspending a bucket from the center of the bridge and gradually filling it with sand. This is a far better result than what was originally predicted. During testing, the bridge failed on the right side directly beneath where the additional truss section ends. Calculations were made for find the compression and tension forces acting on the bridge when weight is added. These calculations were used to predict where the bridge would most likely fail. In conclusion, the maximum weight of 42.3 pounds was a very successful, unexpected result.

            If we were to design another bridge in the future, we would not make any major changes. We are very happy with our final bridge result. However, if we wanted to save money and reduce the overall cost, we could remove some members of the bridge that are not as essential to the bridge’s strength. Another way to cut down on the bridge’s overall cost would be to remove some gusset plates. Our bridge has a lot of joints, I we took out some of these gusset plates, our overall price would be significantly less but so would the amount of weight the bridge can support. If our goal were to increase the amount of weight the bridge is able to support, our main focus would be to add more members. With more members on the bridge, the weight it is supporting will be dispersed among more supports, reducing the total amount of tension and compression on each support.